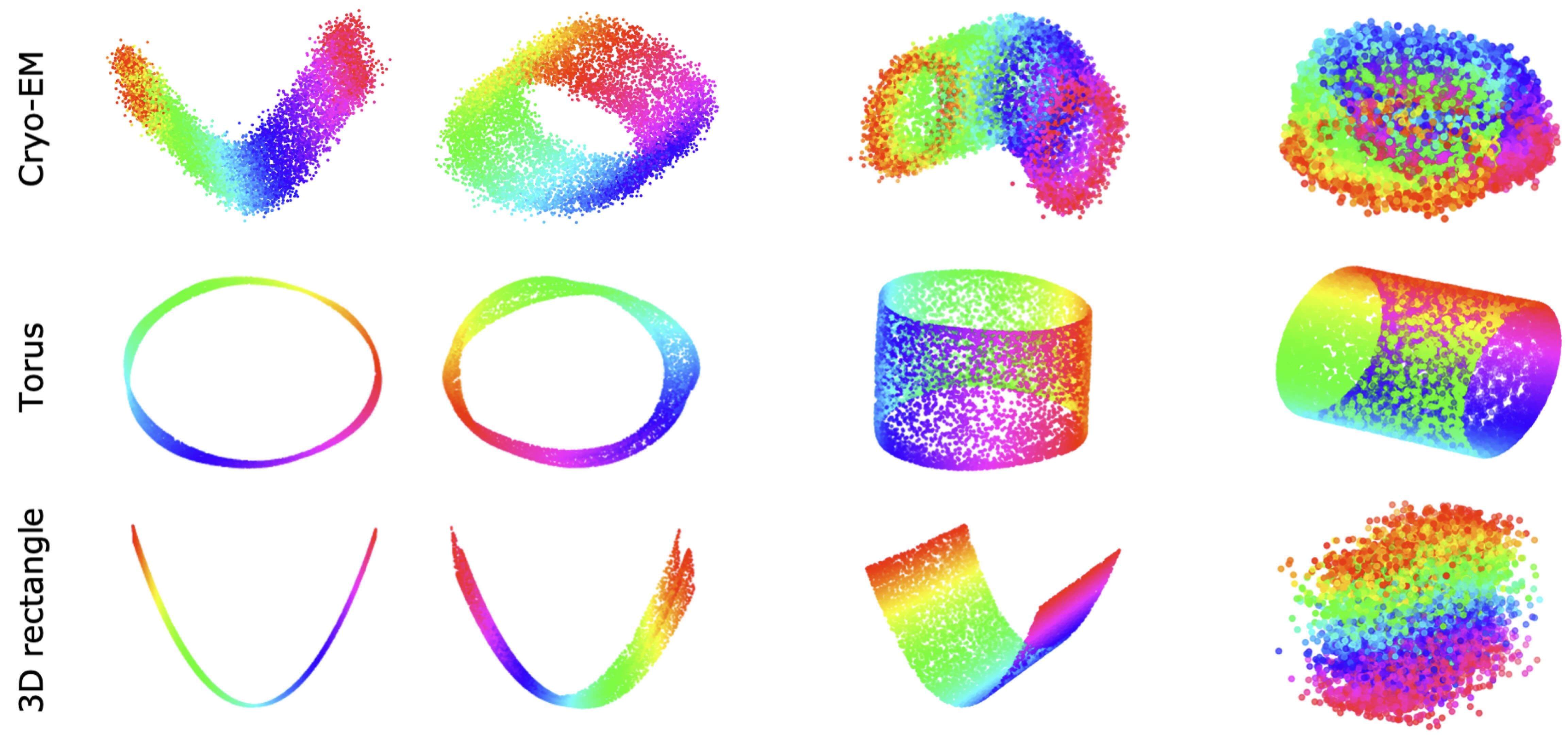Amit Moscovich

Academic homepage

About

I'm a senior lecturer (=tenure-track assistant professor) at the department of statistics and operations research, school of mathematical sciences, Tel Aviv university. Prior to that, I was a postdoctoral research associate at Princeton university's program in applied and computational mathematics, working in Amit Singer's group. I did my Ph.D. at the department of computer science and applied mathematics at the Weizmann institute of science, where Boaz Nadler was my doctoral advisor.

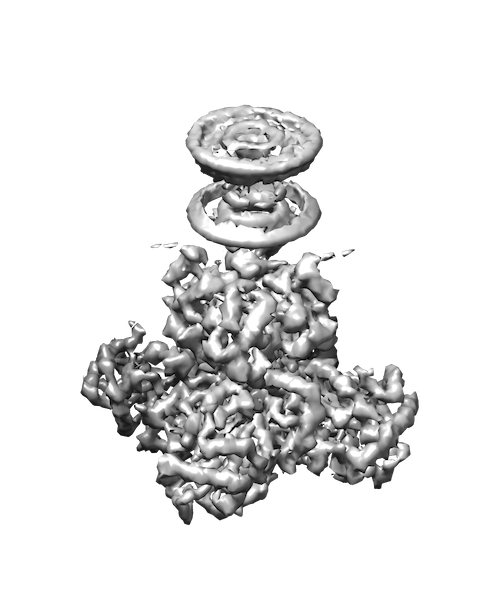
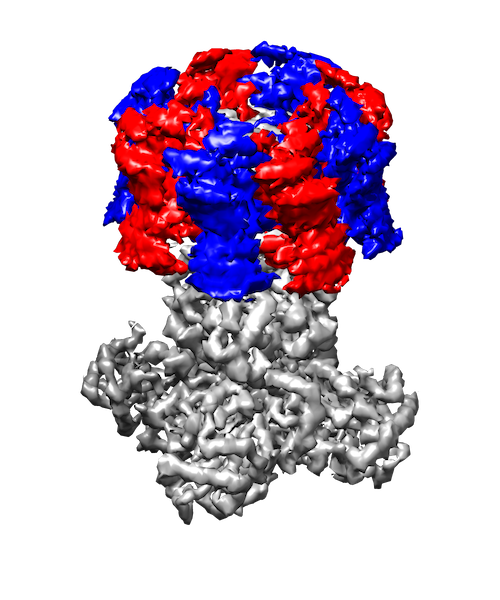
My research interests are broadly in the development of methodology for statistics and machine learning. More specifically, my current focus is developing tools for mapping and analyzing large volumetric data sets. This is motivated by a key challenge in structural biology: the 3D reconstruction and analysis of flexible proteins and other macromolecules from cryo-electron microscopy data sets.

Interested in doing research with me? I sometimes have openings at the MSc/PhD/Postdoc level for people with a strong mathematical foundation. Please email me and we'll setup a meeting.

Video Presentations:
• One-World Cryo-EM talk: Tools for heterogeneity in cryo-EM: manifold learning, disentanglement and optimal transport
• Broad overview of my research (as of 3/2021) at INRIA's DataShape seminar: Nonparametric estimation of high-dimensional shape spaces with applications to structural biology
• Presentation for 3rd year math students at Tel Aviv university (hebrew): Shape spaces, dimensionality reduction and product manifold factorization

Funding:
• Israel Science Foundation (ISF)
• United States-Israel Binational Science Foundation (BSF)
• United States National Science Foundation (NSF)

Address: Schreiber 202, School of Mathematical Sciences, Tel Aviv University.

email Google Scholar Research Gate Github Twitter



Team

Amit Moscovich
Principal investigator


Yeari Vigder
Ph.D. Student


Jonathan Bobrutsky
M.Sc. Student (statistics and data science)


Joseph Kalman (right)
M.Sc. Student (statistics and data science)


Erik Lager
M.Sc. Student (operations research)


Itai Pelles
M.Sc. Student (applied math)



Other Academic Collaborators:
Joakim Andén (KTH Royal Institute of Technology)
Yohai Bar-Sinai (Tel Aviv University)
Alberto Bartesaghi (Duke University)
Tamir Bendory (Tel Aviv University)
Amit Federbush (Tel Aviv University)
Mary Frances Dorn (Los Alamos National Labs)
Amit Halevi (Princeton University)
Ariel Jaffe (Hebrew University of Jerusalem)
Joe Kileel (University of Texas at Austin)
Boaz Nadler (Weizmann Institute of Science)
Rohan Rao (Five Rings Capital)
Saharon Rosset (Tel Aviv University)
Amit Singer (Princeton University)
Clifford H. Spiegelman (Texas A&M)
Yaniv Tenzer (Facebook)
Nathan Zelesko (Northeastern University)
Sharon Zhang (Stanford University)
Ye Zhou (Duke University)




Publications

Amit Federbush, Amit Moscovich, Yohai Bar-Sinai.
Hidden Markov modeling of single particle diffusion with stochastic tethering.
Submitted.
[ preprint | code ]

Amit Moscovich.
Fast calculation of p-values for one-sided Kolmogorov-Smirnov type statistics.
Computational Statistics & Data Analysis (2023).
[ paper | code | tweet ]

Amit Moscovich, Saharon Rosset.
On the cross-validation bias due to unsupervised pre-processing.
Journal of the Royal Statistical Society Series B (2022).
[ paper | code ]

Ye Zhou, Amit Moscovich, Alberto Bartesaghi.
Data-driven determination of number of discrete conformations in single-particle cryo-EM.
Computer Methods and Programs in Biomedicine (2022).
[ paper ]

Joe Kileel, Amit Moscovich, Nathan Zelesko, Amit Singer.
Manifold learning with arbitrary norms.
Journal of Fourier Analysis and Applications (2021).
[ paper | code | tweet ]

Sharon Zhang, Amit Moscovich, Amit Singer.
Product Manifold Learning.
AISTATS 2021.
[ paper | code | tweet | blogpost ]

Rohan Rao, Amit Moscovich, Amit Singer.
Wasserstein K-Means for Clustering Tomographic Projections.
Machine Learning for Structural Biology workshop, NeurIPS (2020).
[ paper | code | video ]

Yaniv Tenzer, Amit Moscovich, Mary-Frances Dorn, Boaz Nadler, Clifford Spiegelman.
Beyond trees: Classification with sparse pairwise dependencies.
Journal of Machine Learning Research (JMLR), 2020.
[ paper ]

Nathan Zelesko, Amit Moscovich, Joe Kileel, Amit Singer.
Earthmover-based manifold learning for analyzing molecular conformation spaces.
IEEE 17th International Symposium on Biomedical Imaging (ISBI), 2020.
[ paper | code ]

Ye Zhou, Amit Moscovich, Tamir Bendory, Alberto Bartesaghi.
Unsupervised particle sorting for high-resolution single-particle cryo-EM.
Inverse Problems, 2020.
[ paper ]

Amit Moscovich, Amit Halevi, Joakim Andén, Amit Singer.
Cryo-EM reconstruction of continuous heterogeneity by Laplacian spectral volumes.
Inverse Problems, 2020.
[ paper | code ]

Amit Moscovich, Ariel Jaffe, Boaz Nadler.
Minimax-optimal semi-supervised regression on unknown manifolds.
Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS), 2017.
[ paper | supplementary | poster | slides | code ]


Amit Moscovich, Boaz Nadler.
Fast calculation of boundary crossing probabilities for Poisson processes.
Statistics & Probability Letters, 2017.
[ paper | poster ]



Amit Moscovich, Boaz Nadler, Clifford Spiegelman.
On the exact Berk-Jones statistics and their p-value calculation.
Electronic Journal of Statistics, 2016.
[ paper | supplementary | code | Python | R ]